Sphere mesh from octahedron subdivision ↩

Metadata 
aliases: []
shorthands: {}
created: 2022-02-27 22:42:31
modified: 2022-02-27 23:03:45

A good way of generating a sphere mesh is to start out from a regular shape in our case, an octahedron and apply triangle subdivision to give it more intermediate vertices. Then project all the vertices into a sphere. This results in a sphere mesh, that has a better uniformity in the distribution of its vertices.

The result of the method is shown by the following figure with subdivision steps. The color of the triangles shows the area of a given triangle.

The ratio of areas between the largest and smallest triangle on the mesh:

Algorithm

The example codes are written in Python and use the separate arrays convention for storing triangle meshes.

This function, generate_octahedron just gives a hardcoded octahedron mesh:

def generate_octahedron(r = 1):
    x = [0, 0, 1, 1, -1, -1]
    y = [0, 0, 1, -1, 1, -1]
    z = [1, -1, 0, 0, 0, 0]
    for n in range(len(x)):
        R = np.sqrt(x[n]**2 + y[n]**2 + z[n]**2)
        x[n] = x[n]/R
        y[n] = y[n]/R
        z[n] = z[n]/R
    i = [0, 0, 0, 0, 1, 1, 1, 1]
    j = [2, 2, 3, 4, 2, 2, 3, 4]
    k = [3, 4, 5, 5, 3, 4, 5, 5]
    return x, y, z, i, j, k

The result of this is this octahedron:

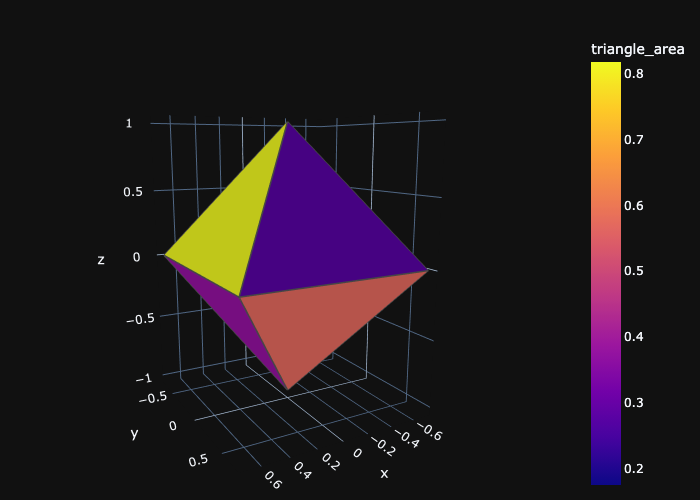
Then with the shown function and the subdivide_triangles function from here, we can give the mesh extra vertices. Finally, by projecting these vertices to a sphere, we get the final result.

x, y, z, i, j, k = generate_octahedron(1)
x, y, z, i, j, k = subdivide_triangles(x, y, z, i, j, k, 4)
for n in range(len(x)):
        R = np.sqrt(x[n]**2 + y[n]**2 + z[n]**2)
        x[n] = x[n]/R
        y[n] = y[n]/R
        z[n] = z[n]/R

So the final result is the first figure on the page.

Notes